
Christophe
Haouy
Site internet adapté à la résolution d'écran 1600 x 900

depuis le 01/09/2014
Since 2014/09/01
Visiteurs
Aucune publicité ne doit apparaître sur ce site. Si ce n'est pas le cas, votre ordinateur est peut-être mal configuré pour les bloquer. Pour observer les images flash, comme Adobe ne les autorise plus, il faut les télécharger et les visaliser avec un logiciel spécialisé ("swf opener" par ex.).
Problèmes
Des problèmes de compréhension sont apparus lors de mon étude de la thermodynamique, de la chimie et de l'hydrodynamique. Je les expose ici, pour témoigner de la difficulté qu'on a tous à analyser les situations ou les réponses données par les spécialistes, quels qu'ils soient. Cela reprend l'esprit de la démarche effectuée dans le document Discussion sur le second principe de la thermodynamique. Ces problèmes sortent du cadre des cours d'initiation donnés sur ce site et sont destinés à des lecteurs qui cherchent à approfondir leurs connaissances en thermodynamique.
Cette rubrique a également pour objectif de partager les interrogations que j'ai eues, espérant qu'elles pourront aider le lecteur à progresser dans l'analyse des problèmes qui lui sont posés.
Cliquer sur un bouton du titre (bleu sur fond blanc) pour accéder à la réponse.
01 - Travail échangé lors d'un dégagement gazeux (réaction chimique)
Question : Calculer le travail effectué par la réaction de 50 g de fer avec du chlorure d'hydrogène dans un bécher ouvert à 25 °C.
Données :
Fe(s) + 2 HCl(aq) donne FeCl2(aq) + H2(g).
Masse molaire du fer : 55,85 g/mol
Constante des gaz parfaits R=8,3145 J/K.mol
Réponse donnée dans Chimie Physique de Peter W. Atkins, de Boeck université, 6ème édition, exemple 2.1. page 54 :
Le gaz repousse l'atmosphère et donc w=-Pext * delta(V). Le volume initial peut être négligé car le volume final (après production de gaz) est très supérieur et delta(V)=Vfinal - Vinitial=Vfinal=nRT/Pext, n étant la quantité de H2 produit. Donc w=- Pext*nRT/Pext=-nRT.
1 mol de H2 est produite pour la consommation d'1 mol de fer. Comme on a 50/55,85 mol de fer on en déduit que l'on a n=50/55,85 d'où W=- 50/55,85 * 8,3145*(273,15 + 25)=-2,2 kJ
Le problème : lorsqu'un gaz s'échappe dans un environnement composé de gaz d'espèces chimiques différentes (air par exemple), il ne voit aucun opposant et se détend comme s'il se détendait dans le vide (bien que l'état stable soit plus lentement atteint que dans le vide) : il s'agit simplement d'une détente de type "Joule". Le gaz se détend jusqu'à ce que sa pression soit égale à celle de la pression de vapeur saturante si rien ne vient limiter son volume.
On peut donc admettre que le H2 produit lors de la réaction chimique ci-dessus n'est pas soumis à la pression Pext de l'air qui est d'une espèce chimique différente (gaz composé de 78 % en volume de N2 et de 21 % de O2 pour l'essentiel). Ainsi, le H2 ne peut pas directement "repousser" l'atmosphère comme le dit Atkins, mais ne fait que "repousser" le H2 de l'air, qui possède une pression très faible (quasiment 0 Pa). H2 se dégage donc quasiment dans du vide (sous-entendu "de H2") : l'expansion du H2 est du type "expansion libre" et le travail échangé avec l'atmosphère est donc nul : pourquoi n'obtient-on pas un travail nul dans ce cas ? Où est donc l'erreur commise dans le raisonnement ci-dessus ?
J'ai beaucoup cherché sur internet une explication, demandé à mes collègues chimistes, sans obtenir de réponse (beaucoup d'entre eux étaient d'ailleurs embarrassés car ils n'avaient jamais réfléchi à la question). Certains auteurs imaginent même une "surface" fictive posée sur le liquide du bécher et qui se déplace à l'instar d'un piston, voire qui "gonfle", lors de la production de H2...ça devient une construction de pensée qui fausse la réalité du dispositif et ne fait, de mon point de vue, qu'évacuer une question légitime.
02 - Chaleur Q évaluée par un diagramme entropique T(S) - réversibilité et quasi-staticité
Pourquoi évaluer la chaleur Q développée lors d'une transformation quasistatique quelconque grâce à un diagramme entropique T(S) ou S(T) qui, en toute rigueur, n'est valable que pour une transformation réversible puisque TdS=dQ uniquement pour les transformations réversibles ?
03 - Rendement du moteur de Stirling
Pourquoi le rendement du moteur de Stirling est-il maximal (= 1 - T1/T2 avec T1 la température, en kelvin, de la source froide et T2 la température de la source chaude) alors qu'il s'agit d'un moteur ditherme différent d'un moteur qui évolue sur un cycle de Carnot. Comme il ne s'agit pas d'un cycle de Carnot - seul cycle ditherme réversible - son rendement devrait être inférieur au rendement maximal.
Moteur Stirling (type bêta)

04 - Eléments, atomes et molécules
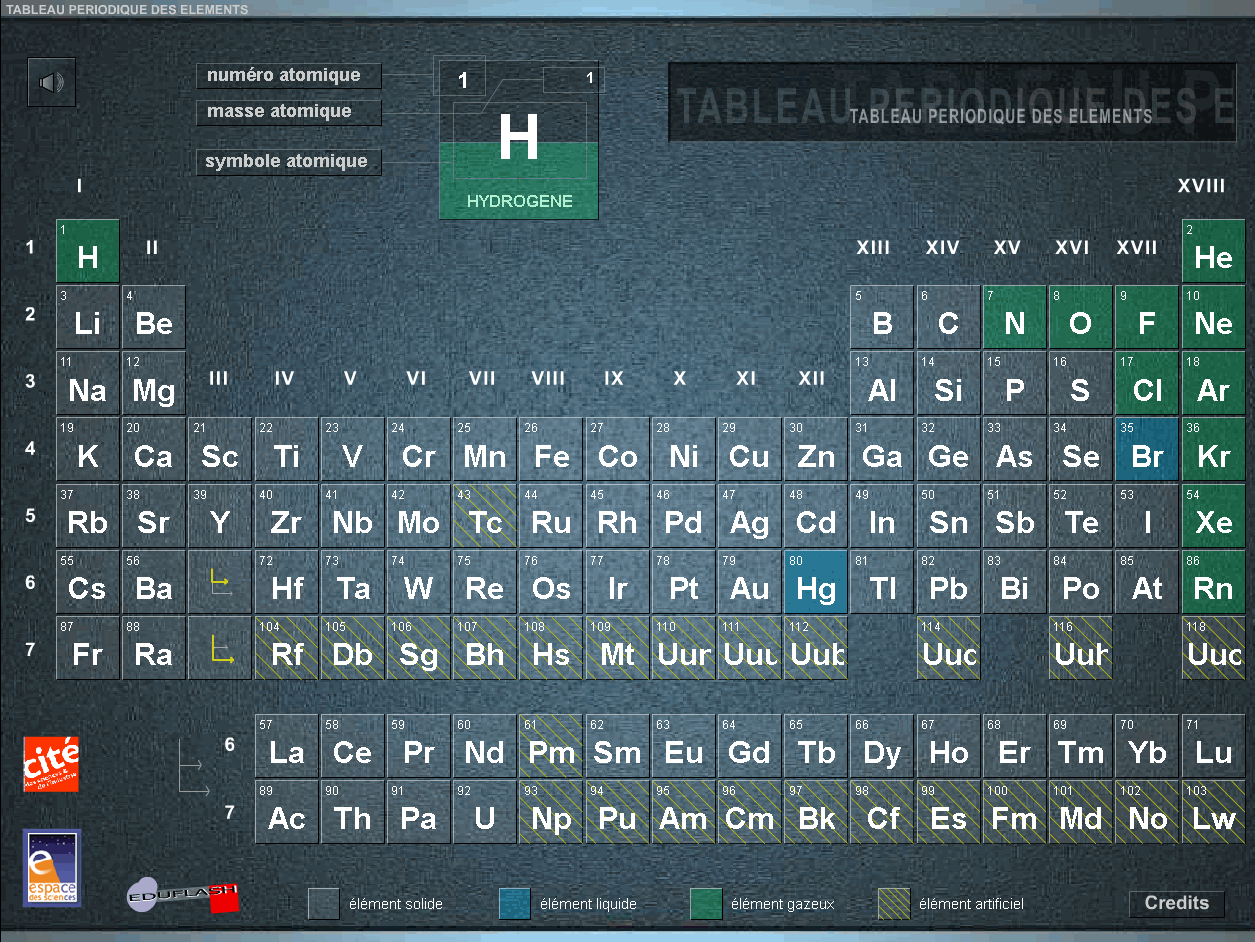
On a beaucoup de mal, quand on commence par étudier la chimie, à distinguer les notions d'élément et d'atomes. Un élément représente le nom attribué à tous les atomes qui possèdent le même nombre de protons mais pas forcément le même nombre de neutrons (isotopes de l'élément). Bien, cependant voilà une image qui représente le tableau périodique des éléments (source : http://www.cite-sciences.fr/archives/francais/ala_cite/expo/tempo/aluminium/science/mendeleiev/mendeleiev.swf) :
L'hydrogène H est, dans ce tableau, classé en tant que "gaz". C'est un problème car l'hydrogène n'est pas un corps particulier : a-t-on déjà vu du gaz hydrogène H dans la nature (à part dans le vide spatial où l'on a des nébuleuses composées d'hydrogène H à raison de moins d'un atome H par cm3) ou même fabriqué artificiellement ? Non, ce qui existe dans la nature matérielle est l'hydrogène combiné à d'autres éléments, comme l'eau (H20), ou bien simplement le dihydrogène H2. Qu'est-ce donc que ce "gaz" dont le nom est H ? De même quel est ce gaz oxygène O, azote N etc... ? En outre la notion de phase d'un corps pur dépend du nombre de particules qui le constituent (voir question 10).
05 - Injecteurs et diffuseurs Venturi
La thermodynamique a parfois partie liée avec l'hydrodynamique. Pourquoi le fait de pincer l'extrémité d'un tuyau d'arrosage (créer un effet "injecteur") permet d'augmenter la vitesse (ou la portée) d'un jet ? En effet la vitesse ne dépend pas de la section de sortie du jet (en absence de pertes de charge) : v=(2*P/µ)^1/2 avec µ la masse volumique de l'eau et P la pression statique effective (c'est-à-dire la pression relative mesurée dans le tuyau buse fermée). La vitesse est donc indépendante de la section de passage de l'eau : le fait de pincer l'extrémité ne devrait pas modifier la portée du jet. Plus techniquement parlant, pourquoi dit-on qu'un "injecteur", une "buse" ou encore une "tuyère" (c'est-à-dire un simple cône convergent placé au bout d'une conduite) permet d'augmenter la vitesse du fluide puisque la vitesse est indépendante de la section de passage du fluide en l'absence de pertes de charge, donnée par la formule de Torricelli v=(2*g*h)^1/2 avec h la hauteur de chute d'eau et g l'accélération de la pesanteur, v est la vitesse "de chute libre".
Des "experts" rencontrés sur les forums internet de physique affirment souvent que c'est dû à la loi de conservation du débit (en régime permanent) : "lorsque la section S diminue la vitesse v augmente car le produit S x v (=débit) est constant par la loi de conservation du débit"...seulement voilà : le débit n'est pas constant lorqu'on ajoute un injecteur ou un diffuseur (injecteur inversé) à l'extrémité du conduit : il diminue en présence d'un injecteur et augmente en présence d'un diffuseur.
Dans le même esprit, pourquoi dit-on qu'un diffuseur Venturi (cône divergent) permet de réduire la vitesse de sortie de l'eau, alors qu'elle est toujours donnée par la formule de Torricelli en l'absence de pertes de charge (vue précédemment), donc indépendante de la section de sortie du cône ?
06 - Détente de Joule - Gay Lussac infiniment lente
On prend une enceinte rigide de volume V2 et calorifugée que l'on sépare en deux compartiments rigides. La détente de Joule-Gay Lussac consiste ici à enfermer un gaz parfait dans un des deux compartiments (de volume V1) puis à pratiquer un trou de taille infinitésimale (pour obtenir une transformation quasistatique) qui communique avec le deuxième compartiment initialement vide : la détente du gaz est isotherme (car dU = dQext + dWext = 0 + 0 = 0 or dU = cste * dT pour un gaz parfait donc dT = 0) et le volume du gaz varie de V1 à V2. La détente est également adiabatique puisque la chaleur Qext échangée avec le milieu extérieur est nulle.
Problème : cette détente est isotherme ou adiabatique ? Si elle est isotherme la pression obéit à la loi P = nRT/V et le point figuratif de la détente dans le plan P(V) se déplace sur une hyperbole. Si elle est adiabatique la pression obéit à la loi PV^(gamma) = Constante et le point figuratif de la détente dans le plan P(V) se déplace sur une courbe différente de l'isotherme. Le point figuratif ne peut pas se déplacer sur deux courbes différentes à la fois...il y a donc un paradoxe.
07 - Détente "quasistatique" de Joule - Gay Lussac et variation d'entropie
On reprend l'expérimentation précédente mais on divise le deuxième compartiment vide en un très grand nombre de sous-compartiments de volumes dV << V1. Chaque sous-compartiment est percé d'un trou de taille infinitésimale à des dates successives, de sorte que le volume de gaz passe très progressivement de V1 à V1+dV etc...jusqu'à atteindre le volume finale V2. Cette détente est donc quasi-statique (chaque volume intermédiaire est parfaitement défini) et isotherme. Lors d'une détente élémentaire, le gaz voit son énergie interne varier telle que dU=TdS - PdV d'où dS=dU + P/T.dV or dU=0 (gaz parfait sur une transformation isotherme) d'où dS=P/T.dV. Comme P=NRT/V pour un gaz parfait on en déduit que dS=NR.dV/V. Ce raisonnement appliqué à toutes les détentes infinitésimales nous amène à affirmer que la variation d'entropie Delta(S) entre l'état initial de gaz (P1, V1, T) et l'état final (P2, V2, T) vaut Delta(S)=NR*ln(V1/V2).
Bien, cela nous amène encore une fois à un problème : on a une transformation quasistatique puisque chaque point intermédiaire de la détente est un point d'équilibre thermodynamique (état stable). On a donc la relation dQ=TdS (valable pour toutes les transformations quasistatiques). Or dQ=0 (pas de transfert thermique interne car la transfo est isotherme sans contact thermique avec l'extérieur, de même il n'y a pas de transfert thermique externe car l'enceinte est adiabatique) d'où dS=dQ/T=0 c'est-à-dire Delta(S)=0 et non Delta(S)=NR*ln(V1/V2) : il y a donc deux résultats différents qui s'affrontent. Où est l'erreur de raisonnement ?
08 - Energie interne
L'énergie interne de n moles de gaz parfait monoatomique à la température T vaut U = 3/2.n.R.T avec R = 8,31 J.K^-1.J^-1 (modèle des gaz rares parfaits par exemple). Cela signifie que lorsqu'on s'approche de T = 0 K, U tend vers 0. Bien, mais Cengel et Boles, dans "Thermodynamique, une approche pragmatique", éditions Chenelière - Mc Graw Hill - De Boeck, affirment p.43 de leur ouvrage que U est la somme de l'énergie cinétique microscopique, de la chaleur latente (énergie de changement de phase), de l'énergie chimique (énergie d'interaction atomique entre noyau et électrons) et de l'énergie nucléaire (énergie de cohésion du noyau). En suivant cette définition de U on ne peut pas avoir U = 3/2.n.R.T car cela signifierait que le gaz parfait disparaît au fur et à mesure que T descend vers 0 K...ce ne peut donc plus être un gaz parfait. Il y a incohérence entre la relation U = 3/2.n.R.T et la définition de U qu'en donnent Cengel et Boles. Où est l'erreur de raisonnement ?
09 - Première loi de Joule - détente de Joule - Gay Lussac
La détente de Joule - Gay Lussac est présentée comme suit ("Thermodynamique", Remi Simon, Belin prépas, paragraphe 8.1.) : un système calorifugé et indéformable est constitué de deux récipients reliés par un robinet. Dans le premier compartiment est placé un gaz parfait, le deuxième compartiment est vide (ou rempli d'un gaz d'une espèce chimique différente). On détent le gaz en ouvrant le robinet. "Puisque la frontière délimitant le système est indéformable et fixe, et parfaitement calorifugée, on a W = 0 et Q = 0. Le premier principe s'écrit donc U2 - U1 = W + Q = 0 + 0 = 0 [...]. Pour un gaz parfait, cela implique que T1 = T2, cela constitue la première loi de Joule".
Problème : en quoi delta U = U2 - U1 = 0 (ou U1 = U2) implique que T1 = T2 pour le gaz parfait ? En d'autres termes, pourquoi U ne dépend que de T ? En outre, si on prend un gaz réel on a encore une fois U2 - U1 = 0 puisqu'on a toujours W + Q = 0 (parois indéformables et calorifugées) : pour le gaz réel on aurait donc U qui ne dépend que de T en suivant la même logique, ce qui est faux. Où se trouve l'erreur de raisonnement ?
A partir de quel moment considère t-on que l'on a un gaz (diazote N2 par exemple) ? En effet, imaginons une enceinte de volume très élevé (volume de la Terre par exemple) et plaçons-y une molécule de diazote : a-t-on un solide, un liquide ou un gaz diazote ? La phase adoptée par un corps pur dépend des interactions (forces de Van Der Waals par exemple) entre les atomes ou molécules de corps. Si on n'a qu'une particule de ce corps dans une enceinte (de volume quelconque d'ailleurs, donc aussi petit qu'on veut à la limite) on ne peut pas avoir d'interaction avec une autre particule : on ne pourrait donc pas pouvoir parler d'état ?
Corrolaire : si l'on place maintenant deux particules du corps pur dans le volume précédent, peut-on alors préciser la phase (gaz, liquide, solide) du corps ainsi formé ?
